We've found a quicker way to multiply really big numbers
- Written by David Harvey, Associate professor in mathematics, UNSW
Multiplication of two numbers is easy, right?
At primary school we learn how to do long multiplication like this:
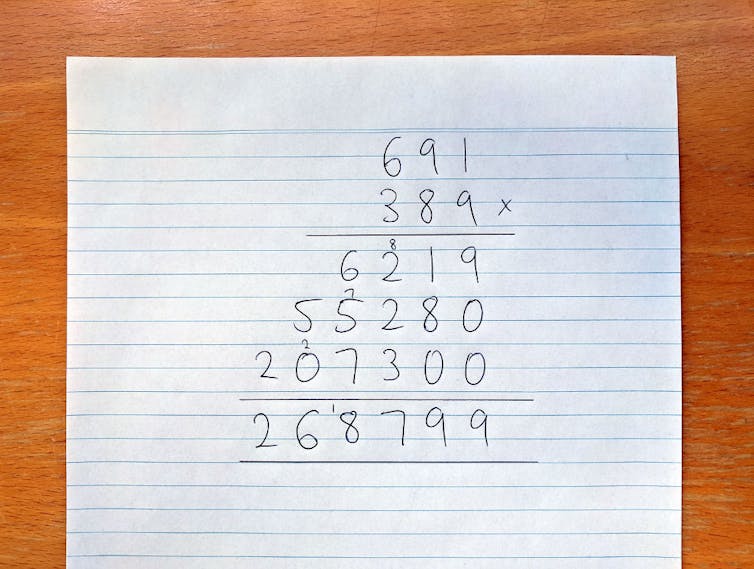 The long way to multiplication.
David Harvey
The long way to multiplication.
David Harvey
Methods similar to this go back thousands of years, at least to the ancient Sumerians and Egyptians.
But is this really the best way to multiply two big numbers together?
Read more: Six images reveal how we ‘see' data and capture invisible science
In long multiplication, we have to multiply every digit of the first number by every digit of the second number. If the two numbers each have N digits, that’s N2 (or N x N) multiplications altogether. In the example above, N is 3, and we had to do 32 = 9 multiplications.
Around 1956, the famous Soviet mathematician Andrey Kolmogorov conjectured that this is the best possible way to multiply two numbers together.
In other words, no matter how you arrange your calculations, the amount of work you have to do will be proportional to at least N2. Twice as many digits means four times as much work.
Kolmogorov felt that if a short cut was possible, surely it would have already been discovered. After all, people have been multiplying numbers for thousands of years.
This is a superb example of the logical fallacy known as “the argument from ignorance”.
A quicker way
Just a few years later, Kolmogorov’s conjecture was shown to be spectacularly wrong.
In 1960, Anatoly Karatsuba, a 23-year-old mathematics student in Russia, discovered a sneaky algebraic trick that reduces the number of multiplications needed.
For example, to multiply four-digit numbers, instead of needing 42 = 16 multiplications, Karatsuba’s method gets away with only nine. When using his method, twice as many digits means only three times as much work.
This stacks up to an impressive advantage as the numbers get bigger. For numbers with a thousand digits, Karatsuba’s method needs about 17 times fewer multiplications than long multiplication.
But why on earth would anyone want to multiply such big numbers together?
In fact, there are a tremendous number of applications. One of the most visible and economically significant is in cryptography.
Big numbers in real life
Every time you engage in encrypted communication on the internet — for example, access your banking website or perform a web search — your device performs a head-spinning number of multiplications, involving numbers with hundreds or even thousands of digits.
Very likely your device uses Karatsuba’s trick for this arithmetic. This is all part of the amazing software ecosystem that keeps our web pages loading as snappily as possible.
For some more esoteric applications, mathematicians have to deal with even larger numbers, with millions, billions or even trillions of digits. For such enormous numbers, even Karatsuba’s algorithm is too slow.
A real breakthrough came in 1971 with the work of the German mathematicians Arnold Schönhage and Volker Strassen. They explained how to use the recently published fast Fourier transform (FFT) to multiply huge numbers efficiently. Their method is routinely used by mathematicians today to handle numbers in the billions of digits.
The FFT is one of the most important algorithms of the 20th century. One application familiar in daily life is digital audio: whenever you listen to MP3s, music streaming services or digital radio, FFTs handle the audio decoding behind the scenes.
An even quicker way?
In their 1971 paper, Schönhage and Strassen also made a striking conjecture. To explain, I’ll have to get a bit technical for a moment.
The first half of their conjecture is that it should be possible to multiply N-digit numbers using a number of basic operations that is proportional to at most N log (N) (that’s N times the natural logarithm of N).
Their own algorithm did not quite reach this target; they were too slow by a factor of log (log N) (the logarithm of the logarithm of N). Nevertheless, their intuition led them to suspect that they were missing something, and that N log (N) should be feasible.
In the decades since 1971, a few researchers have found improvements to Schönhage and Strassen’s algorithm. Notably, an algorithm designed by Martin Fürer in 2007 came agonisingly close to the elusive N log (N).
The second (and much more difficult) part of their conjecture is that N log (N) should be the fundamental speed limit — that no possible multiplication algorithm could do better than this.
Sound familiar?
Have we reached the limit?
A few weeks ago, Joris van der Hoeven and I posted a research paper describing a new multiplication algorithm that finally reaches the N log (N) holy grail, thus settling the “easy” part of the Schönhage–Strassen conjecture.
The paper has not yet been peer-reviewed, so some caution is warranted. It is standard practice in mathematics to disseminate research results before they have undergone peer review.
Instead of using one-dimensional FFTs — the staple of all work on this problem since 1971 — our algorithm relies on multidimensional FFTs. These gadgets are nothing new: the widely-used JPEG image format depends on 2-dimensional FFTs, and 3-dimensional FFTs have many applications in physics and engineering.
In our paper, we use FFTs with 1,729 dimensions. This is tricky to visualise, but mathematically no more troublesome than the 2-dimensional case.
Really, really big numbers
The new algorithm is not really practical in its current form, because the proof given in our paper only works for ludicrously large numbers. Even if each digit was written on a hydrogen atom, there would not be nearly enough room available in the observable universe to write them down.
Read more: Why do we need to know about prime numbers with millions of digits?
On the other hand, we are hopeful that with further refinements, the algorithm might become practical for numbers with merely billions or trillions of digits. If so, it may well become an indispensable tool in the computational mathematician’s arsenal.
If the full Schönhage–Strassen conjecture is correct, then from a theoretical point of view, the new algorithm is the end of the road – it is not possible to do any better.
Personally, I would be very surprised if the conjecture turned out to be wrong. But we shouldn’t forget what happened to Kolmogorov. Mathematics can sometimes throw up surprises.
Authors: David Harvey, Associate professor in mathematics, UNSW
Read more http://theconversation.com/weve-found-a-quicker-way-to-multiply-really-big-numbers-114923



















