Angles and Sides in Geometry
- Written by NewsServices.com

From our previous stints in the topic of geometry, we know different terms such as angle, sides, etc. Angle is the measure of separation between two sides of a geometrical figure or to say more generically it is the measure of separation between two lines. There are different types of angles. Some of which are listed below:
Acute angle: The angles which measure less than 90° are called acute angles. They have their measure anywhere in the range of 0° to 90°, excluding these two measures.
Right angle: The angles which measure exactly equal to 90° are called right angles. If a line is perpendicular on any surface or to any other line then it is said to form a right angle with that surface or line.
Obtuse angle: The angles which measure more than 90° are called obtuse angles. They have their measure in the bracket of (90°, 180°), excluding these two measures.
Straight angle: It is an angle which has its measure exactly equal to 180°. This angle is also referred to as a combination of the acute angle and the obtuse angle.
Supplementary angle: Angles which have their sum is equal to 180° are called supplementary angles. There are various kinds of supplementary angles too which we shall learn later in here.
Complementary angle: Angles which have their sum is equal to 90° are called complementary angles. There are various kinds of complementary angles too which we shall learn later in here.
Reflex angle: Angles which are in the range of 180° to 360° are known as reflex angles. The thing to be noted here is that for an angle to be called reflex angle it should measure more than 180° and less than 360° and not equal to these measures under any circumstances.
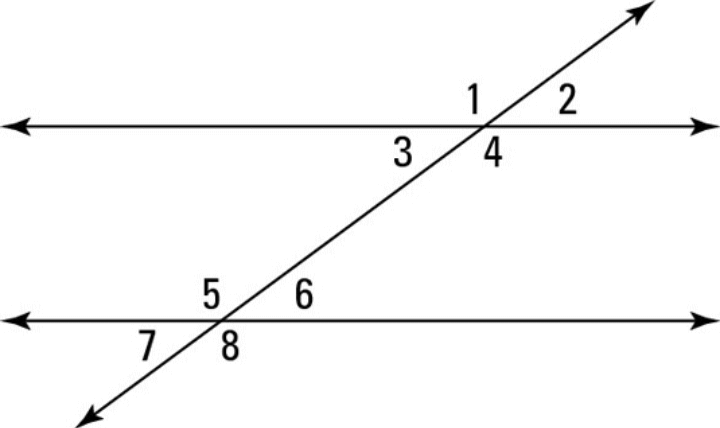
Vertically opposite angles: In the above given figure what we are seeing is a line intersecting two parallel lines. This leads to the formation of a number of angles.
Angles denoted by the numbers (2,3), (1,4), (6,7) & (5,8) are vertically opposite angles. As they are opposite to each other on a vertical line.
Corresponding angles: In the above given figure what we are seeing is a line intersecting two parallel lines. This leads to the formation of a number of angles. Angles denoted by the numbers (2,6) & (1,5) are corresponding angles.
Interior alternate angles: In the above given figure what we are seeing is a line intersecting two parallel lines. This leads to the formation of a number of angles. Angles denoted by the numbers (3,6) & (4,5) are interior alternate angles.
Exterior alternate angles: In the above given figure what we are seeing is a line intersecting two parallel lines. This leads to the formation of a number of angles. Angles denoted by the numbers (1,8) & (2,7) are exterior alternate angles.
Association with triangles:
There is a great deal of association of angles with triangles. It is rampant to such an extent such that a number of triangles are named after the angles present in them. Let us see some of those types of triangles:
Acute triangle: In acute triangle all the angles that are present within it have their measure less than 90°. Sum of all three angles of this type of triangle is equal to 180°.
Obtuse triangle: In an obtuse triangle one of the angles measures more than 90° while the remaining two have their respective measures less than 90°. Sum of all three angles of this type of triangle is equal to 180°.
Right triangle: In the right triangle one of the angles exactly measures 90° while the other two measure less than 90° each. Sum of all three angles of this type of triangle is equal to 180°.
Conclusion:
Careful examination of the facts and details mentioned above regarding angles fetches us a lot of interesting insights. It also lets us know about the different types of angles, their properties etc. Additionally, we also came to know about a number of triangles which are named after angles and their respective property. If you intend to learn more about angles and its different types, you can visit Cuemath.
























